Discount Rate - Valuation
- Luis Valini Neto
- Nov 6, 2024
- 6 min read

Discount Rate - Valuation
The discount rate is the minimum rate of return expected for an investment, taking into account its risk profile. To estimate the present value (PV) of future cash flows generated by a company, an appropriate discount rate is applied - more specifically, the opportunity cost of capital, which reflects the risk underlying the company (or investment). Discount Rate - Valuation
How to calculate the discount rate?
The discount rate, commonly referred to as the "cost of capital," is the minimum rate of return required to invest in a specific project or investment opportunity.
In corporate finance, the discount rate represents the expected return on an investment, such as common stock, considering the risk of future cash flows.
Conceptually, the discount rate estimates the risk and possible returns of an investment - therefore, a higher rate indicates greater risk, but also a higher return.
Interest can be earned over time if the capital is invested today. Thus, the discount rate is often considered the opportunity cost of capital and serves as a hurdle rate to guide decision-making regarding capital allocation and the selection of worthwhile investments.
When analyzing an investment, the rate of return an investor can expect to earn depends on the returns of comparative investments with similar risk profiles.
You can calculate the discount rate using three steps.
Start by dividing the future cash flow (FV) by the present value (PV).
Take the result from the previous step and raise it to the power of the reciprocal of the number of years (1 ÷ n).
Subtract one from this final value to get the discount rate.
Discount rate formula
The discount rate formula divides the future value (FV) of a cash flow by its present value (PV), raising the result to the reciprocal of the number of periods and subtracting one.
Discount Rate (i) = (Future Value ÷ Present Value) ^ (1 ÷ n) – 1
Suppose your investment portfolio has grown from $10,000 to $25,000 over eight years.
Future Value (FV) = R$ 25,000
Present Value (PV) = R$ 10,000
Number of Periods = 8 years
If we consider these assumptions in the formula, the discount rate will be around 12.14% per year.
Discount rate (i) = ($25,000 ÷ $10,000) ^ (1 ÷ 4) – 1 = 12.14%
The example in question shows an annual capitalization, that is, once a year.
However, if we consider semi-annual capitalization (twice a year), we multiply the number of periods by the capital frequency.
Considering the effects of capitalization, the discount rate will be 5.89% over six months.
Discount Rate (i) = ($25,000 ÷ $10,000) ^ (1 ÷ 16) – 1 = 5.89%
Discount Rate vs. Net Present Value (NPV): What's the Difference?
The net present value (NPV) of a future cash flow is the amount of cash flow discounted to the present date.
Thus, a higher discount rate reduces the present value (PV) of future cash flows (and vice versa)
Discount Rate = (Future Value ÷ Present Value) ^ (1 ÷ n) – 1
The further away the receipt of cash flow is, the greater the reduction will be.
Furthermore, it is important to consider that increased risk must coincide with a higher return potential.
Higher Discount Rate → Lower Net Present Value (NPV)
Lower Discount Rate → Higher Net Present Value (NPV)
In this way, the expected return is set higher to compensate investors who took on the risk.
If the expected return is insufficient, it would not be reasonable to invest, as there are other investments that offer a better risk/return ratio.
On the other hand, a lower discount rate increases the valuation, as such cash flows are more certain to be received.
In other words, future cash flows are more stable and likely to occur in the foreseeable future. As such, stable, market-leading companies like Amazon and Apple tend to have lower discount rates.
Learn more → Discount rate by sector (Damodaran)
Why is the discount rate important?
In a Discounted Cash Flow (DCF) analysis, the discount rate is key to determining the intrinsic value of an investment, usually a company. The DCF model calculates the present value (PV) of projected future cash flows, which are then “discounted” to reflect their current value. Adding all of the discounted future cash flows together, we have the implied intrinsic value of an investment.
Since the discount rate reflects the risk and the required return, it is one of the main variables in DCF analysis. An important principle is that the discount rate should be aligned with the perspective of the investment stakeholders.
Weighted Average Cost of Capital (WACC): Reflects all stakeholders (both creditors and shareholders).
Cost of equity Common shares (ke): Belongs to ordinary shareholders.
Cost of Debt (kd): Represents creditors.
Cost of Preferred Shares (kp): Specific to preferred shareholders.
WACC vs. Cost of Equity: Key Differences
The weighted average cost of capital (WACC) shows the return that all providers of capital—both debt and equity holders—expect on their investment. Because WACC includes both debt and equity, it is used to discount free cash flow to the firm (FCFF), which represents the cash flow available to both types of investors.
The cost of equity is the minimum return expected by shareholders alone. Therefore, free cash flow to equity (FCFE), which belongs specifically to shareholders, must be discounted using the cost of equity because it represents returns to common shareholders only.
In an unlevered DCF, the firm's FCFF is projected and discounted using the WACC. In contrast, a levered DCF estimates the firm's FCFE and uses the cost of equity as the discount rate.
Components of the WACC Discount Rate
The Weighted Average Cost of Capital (WACC) represents the opportunity cost of investing in assets with similar levels of risk.
According to the formula, WACC is calculated by multiplying the equity weight by the cost of equity and adding it to the debt weight multiplied by the tax-affected cost of debt.
WACC = [ke × (E ÷ (D + E))] + [kd × (D ÷ (D + E))]
Where:
E / (D + E) = Equity Weight (%)
D / (D + E) = Debt Weight (%)
ke = Cost of Equity
kd = After-Tax Cost of Debt
From the Cost of Debit we deduct the tax rate to find the Net Cost of Debito
After-Tax Cost of Debt (kd) = Cost of Debt × (1 – Tax Rate %)
Calculating the Cost of Equity with the CAPM
Based on the Capital Asset Pricing Model (CAPM), the expected profitability of an asset is determined by three main factors:
Risk Free Rate : This is the expected return on a risk-free investment, such as a government bond. It represents the expected base return without risk being involved.
Market Risk Premium : This is the additional return expected from investing in a riskier asset (such as stocks) compared to the risk-free rate. The market risk premium reflects the return that investors demand for taking on additional risk.
Asset Beta : Beta measures how much an asset’s return varies relative to the market as a whole. If an asset has a beta greater than 1, it is more volatile than the market, meaning it can offer higher returns but also comes with more risk. On the other hand, a beta less than 1 indicates that the asset is less volatile than the market.
Cost of Equity (ke) =
Risk Free Rate + Beta × Market Risk Premium
Spreadsheet for calculating WACC
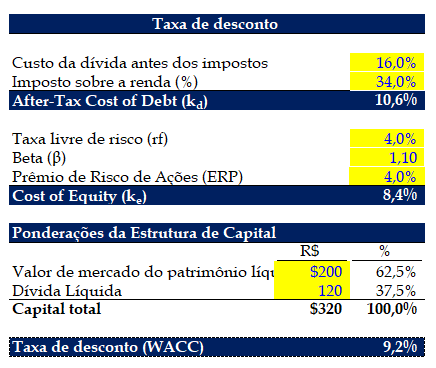
Example of Calculating the Cost of Debt Capital (kd)
Suppose we need to calculate the weighted average cost of capital (WACC) for a firm.
The first step is to calculate the cost of debt.
If we assume the firm has a pre-tax cost of debt of 16% and the tax rate is 34.0%, the after-tax cost of debt is 10.6%.
After-Tax Cost of Debt (kd) = 16% × (1 – 34.0%)
kd = 10.6%
Example of Calculating the Cost of Equity (ke)
The next step is to calculate the cost of equity using the capital asset pricing model (CAPM).
The three assumptions for our three input data are as follows:
Risk Free Rate (rf) = 4.0%
Beta (β) = 1.10
Equity Risk Premium (ERP) = 4.0%
If we plug these values into the CAPM formula, the cost of equity will be 8.4%.
Cost of Equity (ke) = 4.0% + (1.10 × 4.0%)
ke = 8.4%
Capital Structure Analysis Example
Now we must define the weights of the capital structure, that is, the percentage contribution of each source of capital.
The market value of equity – that is, the market capitalization (or equity value) – is assumed to be R$200 million. On the other hand, the company's net debt is assumed to be R$120 million.
Market Value of Equity = R$200 million
Net Debt = R$120 million
Adding the R$200 million in equity value and the R$120 million in net debt, we calculate that the company's total capital (own and third-party) is R$320 million.
From this $320 million, we can determine the relative weights of debt and equity in the company's capital structure:
Equity Weight = 62.5%
Debt Burden = 37.5%
Discount Rate Calculation Example
From now on, we have the necessary information to calculate the company's discount rate, calculated by adding the costs of each source of capital plus the corresponding weight of the capital structure.
Discount Rate (WACC) = (10.6% × 37.5%) + (8.4% × 62.5%)
WACC = 9.2%
To conclude, our hypothetical company's discount rate (or cost of capital) is 9.2%, which is the implicit rate used to discount its future cash flows.
Luis Valini


Comments